Разметчик Фибоначчи и его использование при изготовлении мебели.

Разметчик Фибоначчи - это устройство, позволяющее вам всегда иметь под рукой соотношениие размеров для ваших изделий, удовлетворяющее принципам Золотого Соотношения. Если вы хотите, чтоб мебель, которую вы делаете, была не только функциональна, но и по-настоящему красива, то начинать нужно с пропорций предмета в целом и его частей. Если эти пропорции правильны, ваше произведение будет радовать глаз, иначе - может быть ужасным. Разметчик Фибоначчи - отличное подручное средство для проектирования красивых изделий.

Разметчик Фибоначчи, специальный инструмент, назван по имени итальянского математика Фибоначчи, жившего в  XIII веке.  "Фибоначчи" у этого учёного - это псевдоним, происхождение которого не известно он же - Fibonacci, он же - Леона́рдо Пиза́нский, он же - Leonardo Pisano. В честь учёного назван и числовой ряд, в котором каждое последующее число равно сумме двух предыдущих. Эта числовая последовательность носит название чисел Фибоначчи: 0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233, 377, 610, 987, 1597, 2584, 4181, 6765, 10946, 17711, 28657, 46368, 75025, 121393, 196418, 317811, 514229, 832040, …  Хотя этот ряд и был известен ещё в Древней Индии, т.е. задолго до рождения умного Фибоначчи, но, тем не менее, своё нынешнее название числа Фибоначчи получили благодаря исследованию свойств этих чисел, проведённому именно этим учёным в его труде «Книга абака» (Издательство РИМГНИЗ "Римское Государственное Народное Издательство", 1202 г.).  Ряды Фибоначчи, спирали Фибоначчи, уровни Фибоначчи - об этом много можно прочитать.

К чёму всё это? Одна закономерность упомянута, но можно заметить и другую - деление числа в ряду Фибоначчи на предыдущее даёт практически постоянный результат - 1,618 - проверьте, если не лень. С этими последовательностями много чего связано - от биржевых котировок до рубежей разграничения развития человечества на отдельные этапы, которые иногда называют временными ступенями эволюции. Короче говоря, замечательная последовательность. Ну и к чему же это, нам то, с шипорезками, пилами и стамесками, зачем всё это? Есть в этом большой смысл и для нас, читаем дальше.

Даже если вы одарены превосходным видением, не так-то просто спроектировать предмет мебели без использования основополагающих принципов для определения размеров этого предмета мебели и, главное, пропорций между его элементами. Будет ли это подход к проектированию, который передаётся от мастера к ученику или ваше врожденное чувство равновесия и гармонии, которым обладают лишь некоторые одарённые люди, в любом случае без такой совокупности знаний и опыта вы не сможете создать совершенное изделие, которое будет радовать ваш глаз и вызывать восхизение окружающих и ваших друзей. Можно создать изделие, которое будет прочно и функционально адекватно, но не будет радовать и вызывать приятные чувства. Предмет мебели, который не учитывает проверенные веками правила построения может выглядеть неуклюжим, неуравновешенным или даже ужасным.

Главным среди множества совокупностей фундаментальных установок, сложившихся за сотни лет представлений и понятий, которые разработчики предметов мебели использовали и продолжают использовать  для обеспечения баланса и хороших пропорций в дизайне мебели является золотая пропорция или соотношение (также называемое золотой серединой или золотым сечением). Обозначается эта пропорция греческой буквой ∳ (фи). Золотое соотношение может быть выражено уравнением ∳ (фи)= [1 + √ 5] / 2. Для простоты практического применения, мы можем взять лишь результирующее значение ∳ (фи), равное 1,618. Т.е. одно значение к другому должно относится как 1 к 1,618. Одна длина, к другой, например.

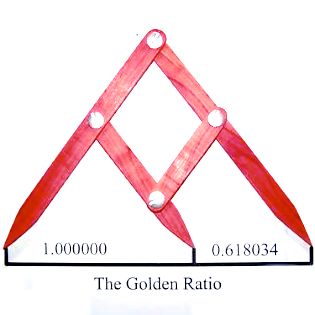
Один из многих замечательных принципов золотой пропорции является то, что коротий отрезок прямой линии по отношению к длинному отрезку этой же линии относится так же, как длинный отрезок линии относится к общей длине линии, и это соотношение равно ∳ (фи) = 1,618:

Именно это соотношение заложено в самой конструкции замечательного разметочного инструмента - Разметчика Фибоначчи:

Исходя из описанного принципа, Золотым (или гармоничным) Прямоугольником является такой, стороны в котором соотносятся как 1 : 1,618, т.е. длина большей стороны прямоугольника равна длине меньшей стороны прямоугольника, умноженной на ∳ (фи)=1,618:

Узнаёте? Это же столешница гармоничного стола! Или фасад тумбы и много чего ещё.

Аналогично, Золотым (или гармоничным) Параллелепипедом является тот, стороны в котором тоже соотносятся как 1 : 1,618, т.е. длина большей стороны параллелепипеда равна высоте параллелепипеда, умноженной на ∳ (фи)=1,618, а ширина параллелепипеда равна высоте параллелепипеда, поделённой на ∳ (фи)=1,618:

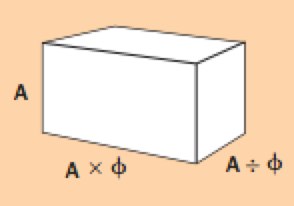
Узнаёте? Это же мебельная тумба, пристенный стол (консоль) и т.д.

Золотая Пропорция лежит в основе многих (если не всех) естественных соотношений и даже построения нашей Вселенной. Примеры есть в изобилии на каждом уровне, от размножения кроликов, расположения семян в подсолнухе и орешков в шишке, до астрофизики и квантовой механики. Планетарные орбиты и даже структура человеческой фигуры являются ещё одним подвержедния соблюдения этой замечательной пропорции.

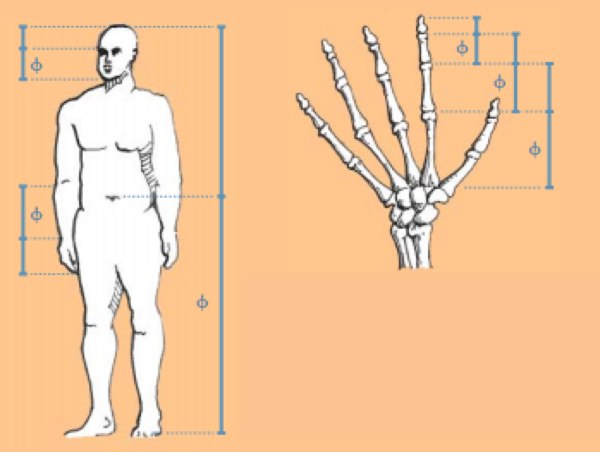
Соотношение между соседними фалангами пальцев - это ∳ (фи) = 1,618, Соотношение между локтем и кистью - это ∳ (фи) = 1,618, соотношение расстояния от макушки до глаз и растояния от глаз до подбородка - это ∳ (фи) = 1,618, соотношение расстояния от макушки до пупка и растояния от пупка до пяток - это опять-таки ∳ (фи) = 1,618:

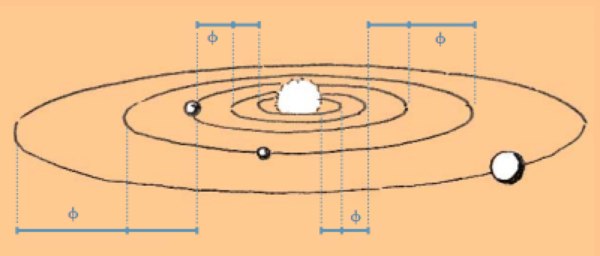
Дистанции между солнцем и первыми пяти планетами в солнечной системе так же соотносятся (примерно) как ∳ (фи) = 1,618, поэтому, как безусловно известно, астронометрия использует золотое соотношение при определении планет на их орбитах:

Будучи столь фундаментальным и столь широко распространённым в природе, это отношение просто призывает нас на подсознательном уровне как абсолютно правильное, которому надо следовать. Как таковое, это соотношение было использовано на протяжении веков дизайнерами и архитекторами, от пирамид до мебельных шедевров.

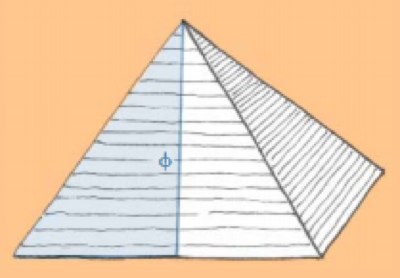
Большая пирамида в Гиза, как теперь понятно, тоже построена в соответствии с Золотым Сечением: высота стороны пирамиды равна длине основания стороны пирамиды, умноженной на всё ту же величину ∳ (фи) = 1,618:

При строительстве Парфенона (древнегреческий храм, расположенный на афинском Акрополе, главный храм в древних Афинах) использовалось соотношение ∳ (фи) = 1,618 при определении внешних размеров и соотношения его частей:

Достоверно не известно, применялись ли при построении Парфенона калькуляторы или Разметчики Фибоначчи, но соотношение точно применялось. Более подробно о соотношении ∳ (фи) = 1,618 в конструкции этого памятника архитектуры сказано в видеоролике, начиная с 48-й секунды:

В вышеприведённом ролике, наконец-то, дело дошло и до предмета мебели, пусть и простого. Главное - соотношение всё то же - ∳ (фи) = 1,618.

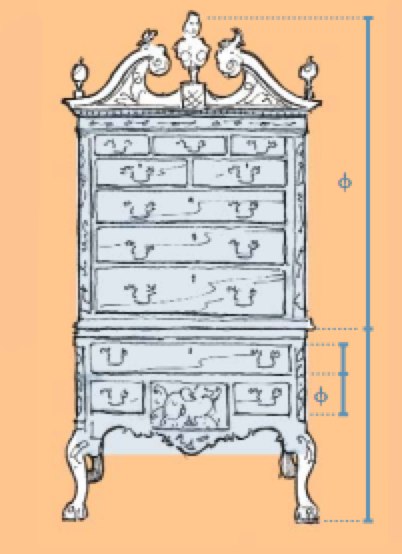
В одном из видов комода с множеством ящиков называемом в разных изданиях как Highboy или Popadour ("Высокий парень" или "Помпадур"), сделанном в Филадельфии в промежутке между 1762 и 1790 годами, используется Золотая Пропорция в соотношении размеров многих из его элементов. Каркас - это Золотой прямоугольник, положение сужения ("талии" шкафа) определяется делением общей высоты шкафа на ∳ (фи) = 1,618. Высоты нижних ящиков так же соотносятся как ∳ (фи) = 1,618:

Золотое Сечение применяется при изготовлении мебели чаще всего в качестве некоего прямоугольника, который строится с помощью ∳ (фи) = 1,618 для двух его измерений, т.е. уже упоминаемого Золотого прямоугольника, где длина в 1,618 раз больше ширины (или наоборот). Эти пропорции могут быть использованы для определения габаритных размеров мебели, а также деталей интерьера, таких как двери и ящики. Можно применять рассчёты, деля и умножая на такое "круглое" и удобное число, как 1,618, но можно просто использовать Разметчик Фибоначчи, просто снимая размеры бОльшего предмета и откладывая после этого размер меньшего предмета. Или наоборот. Быстро, просто и удобно.

Предметы мебели являются трехмерными и Золотое Соотношение может быть применено ко всем трем измерениям, т.е. предмет мебели становится Золотым Параллелепипедом, если сделать его по правилам Золотого Соотношения. К примеру, в простом случае, глядя на предмет мебели сбоку, его высота может быть наибольшим измерением в Золотом  Прямоугольнике. Однако, если смотреть на тот же предмет мебели спереди, та же высота может быть коротким измерением в Золотом Прямоугольнике.

Необходимо отметить, однако, что форма предмета должна следовать за его функцией. Даже превосходные пропорции мебели могут оказаться быть бессмысленными, если этот предмет не может быть использован, например потому, что он слишком маленький или слишком большой или по другим причинам не может быть использован с комфортом. Следовательно, практические соображения должны быть на первом месте. В самом деле, большинство проектов мебели требуют, чтоб вы начали проектирование с некоторых заданных размеров: стол должен быть определенной высоты, шкаф возможно, придется приноравливать к конкретному пространству, а в книжном шкафу может потребоваться определенное количество полок. Но почти наверняка вы вынуждены будете определять множество других размеров, в отношении которых можно применить правильные пропорции. Но результат будет стоит затраченных усилий, чтоб в результате увидеть, как Золотое Соотношение может работать для всех этих элементов. Принятие решения о размерах "на глаз" или, что еще хуже, исходя из имеющихся заготовок, не позволит вам получить отлично сбалансированный, с красивыми пропорциями отдельных частей и предмета мебели в целом.

Итак, размеры отдельных частей мебели должны быть пропорциональны в соответствии с Золотым Соотношением. Такие элементы, как ножки стола, относительные размеры элементов каркаса, такие как вертикальные и горизонтальные части фасадов, проноги, царги и т.д., могут быть рассчитаны с применением Золотой Пропорции. Золотое сечение также предлагает один из способов решение проблемы проектирования ящиков в комоде с ступенчатым увеличением высоты ящиков. С помощью Разметчика Фибоначчи легко осуществить такую разметку - надо просто взять размер бОльшего ящика и по разметчику отложить размеры двух соседних ящиков и т.д. После этого, взяв размер ящика, по разметчику отложить расстояние от верха ящика до места расположения его ручки.

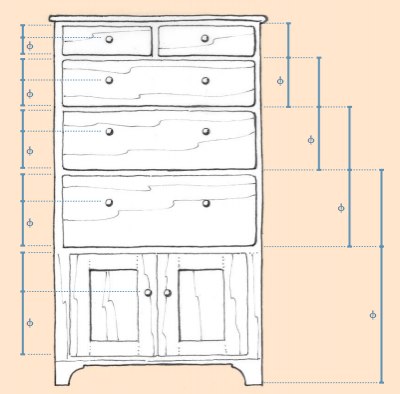
Такой метод использования Разметчика Фибоначчи, как инструмента для практического применения Золотого Соотношения будут эффективен для определения и других размеров, таких, как положение полок в шкафу, разделителей между ящиками и т.д. Любые размеры предмета мебели, изначально, определяются функциональными и структурными требованиями, но множество поправок может быть сделано путём применения Золотого Соотношения, что, несомненно, добавит в предмет гармонию. Использование Золотого Соотношения при проектировании мебели позволит вам сделать гармоничным не только предмет в целом, но и позволит вам быть уверенным в том, что все составные части - дверные панели, ящики, ножки, царги и т.д. принципиально, гармонично связаны между собой.

Спроектировать что-то с абсолютно совершенными пропорциями редко удается в реальности. Почти каждый предмет мебели или дерева придётся соотносить с ограничениями, накладываемыми функциональностью, возможностями столярных соединений или  экономией средств. Но даже попытка приблизиться к совершенству, которое может быть определено как размеры, в точности соответствующие Золотому Соотношению гарантирет вам получение лучшего результата по сравнению с разработкой без внимания к этим основополагающим принципам. Даже если вы приблизились к идеальным пропорциям, то глаз зрителя сгладит небольшие недостатки и сознание заполнит некоторые пробелы в дизайте. Желательно, но не обязательно, чтоб всё было идеально и соответственно формуле. Но если предмет вашей мебели абсолютно не соответствует правильным пропорциям, без сомнения, он будет некрасив. Поэтому стремиться к правильным пропорциям необходимо.

Наконец, мы часто корректируем вещи на глаз, чтобы сделать предмет легче и лучше сбалансированным, и делаем мы это с помощью методов, которые являются повседневными в деревообработке. Эти методы включают в себя учёт изменения размеров заготовки, исходя из направления волокон древесины, учёт рисунка древесины, с помощью которого можно предмет мебели сделать более привлекательным, отделку краёв и углов, которая создаст впечатление большей или меньшей толщины элемента изделия, использование молдингов для более точного соответствия изделия Золотому Прямоугольнику или Параллелепипеду, использование сужающихся ножек, чтобы сделать ощущение большего приближения предмета мебели к идеальной пропорции, и, в конце концов, смешивание всех этих методов для достижения идеального дизайна. Использование Золотого Сечения и инструмента для его применения - Разметчика Фибоначчи - начало этого стремления к совершенству.

В статье использованы материалы главы "A Guide to Good Design" из книги "Practical Furniture Design", написанной Graham Blackburn - признанным мебельным мастером, популяризатором деревообработки и издателем.

Евгений Фукс

технический консультант
LeighJigs.ru
LeighJigsINFO@gmail.com